SIMILAR FOLDS
They are formed by flowage along indiscrete shear surfaces and not by buckling instability as most other folds are. The shear surfaces are not discrete observable ones and cannot be seen at all in naturally developed similar folds unless there are dislocations along axial plane, during late stages of folding when the material passes into brittle field with drop in temperature. Similar folds are restricted usually to the central parts of orogenic belts where strain states are high on account of higher temperatures and pressures.
Figure given in here schematically shows how a similar fold is formed from an original undeformed layer. In buckle folds, the cleavage is parallel to the axial planes of folds and in majority of cases it forms parallel to the principal l1 l2 plane of the finite strain ellipsoid. In similar folds also the cleavage is axial planar but the cleavage planes are not parallel to the principal l1l2 plane of the finite strain ellipsoid but it is parallel to the l= 1 plane of the finite strain ellipsoid. This plane is the one of no finite longitudinal strain or plane along which shear strains are maximum Fig given explains this fact and shows how a dextral shear occurs in the right limb of the antiform and a sinistral one in the left one of it. In reality, this does not happen, only one shear sense may operate but the amount of shear so varies as to give rise to similar folds. The figure is therefore purely hypothetical. But in two limbs, the surfaces of no finite longitudinal strain are different since the sense of displacement in the two limbs is different.
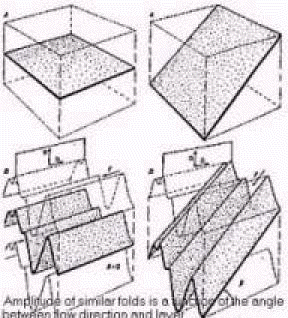
SIMILAR FOLDS, AMPLITUDE
The amplitude of similar folds is determined by the angle d that the layer boundaries make with the future hinge direction. If this angle is zero, then high amplitude similar folds are formed (see Fig.). If the angle is large as shown in the figure, low amplitude structures are formed. If the angle is 90, the inhomogeneous simple shear occurs within the plane itself and no folds are produced. Only the layer boundaries show different curvatures