STEREOGRAPHIC PROJECTIONS
All circles on the sphere plot as circles on the plane, making it easy to construct the projection. The projection preserves angles and small shapes on the sphere project true on the plane. Since no spherical projection allows both area and shape to be conserved, there is distortion. Small regions on the sphere project true on the plane, making the stereographic a good map projection for small areas, but radial distortion increases away from the point of tangency.
In principle, the entire sphere can be projected except for the projection point. In reality the areal distortion in the far hemisphere is high for practical purposes (although extended stereonets have been constructed and used.) In most geological applications we use only the near hemisphere (where areal distortion is not much less) and deal with points in the far hemisphere in one of two ways by projecting the point through the center of the sphere and plot it, using some symbol or annotation to denote that the point is on the other side of the sphere. This is the more common approach; or projecting the point orthographically toward the plane onto the other side of the sphere and plot it, again using some symbol or annotation to denote that the point is on the other side of the sphere, as in mineralogy.
Nets can be constructed by using a spreadsheet with graphing capability and a drawing program such as MS Paint, to copy and flip the drawings or images.
In the spreadsheet, create a table of latitude and longitude. For latitude 90 you only need one longitude (say 0). For latitudes 0-80 degrees, tabulate longitudes from 0 to 90 degrees. We will use this method to construct only one quadrant. Plotting at intervals less than 5 degrees is not recommended. If you plot at 10 degree intervals you will have 91 entries 0,0 - 0, 10, - ... 90,0. If you plot at 5 degrees you will have 421 entries.
Create columns for x,y,z, X and Y. Enter the appropriate formulas and copy them down the columns.
Define a graph area, select an X-Y point plot, and graph X and Y. The result should look recognizably like the desired net. If it doesn't, check your formulas, graph setup, data fields, and so on. Scale the graph so it is as correct in size and proportions as possible.
Export the graph as a graphics file. Most spreadsheets will allow you to block in the graph or the cells around it and use Control-C to copy it. Others have menu options for exporting graphs. Save the spreadsheet.
Go to the drawing program and import the graph. Scale the drawing to the correct proportions and construct the great and small circles. When the quadrant is complete and correct, copy it and flip it as needed to generate the other quadrants.
Stereographic Projection
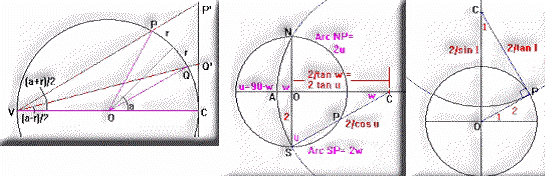
The proof here is not a completely rigorous one but it should convince you that the basic property of the stereographic projection is true. A plane (blue) cuts the sphere to form a small circle with diameter PQ. P and Q project onto the projection plane at P' and Q'.
Proof:
Let the angular diameter of the small circle be 2a and its angular distance from the point of tangency be 2u. Then the angles measured from V, the projection point, are a and u, respectively.
Triangles VOP and POQ are both isoceles. Their base angles are therefore equal and of course their angles sum to 180 degrees. Thus angle VPO = a + u, and OPQ = 90 - a.
From the above results, angle QPP' = 90+u
Triangle VCQ' is a right triangle, therefore angle CQ'V=90-u and angle VQ'P=90+u
Although not shown for reasons of clarity, angle PQV is easy to find. We know the other angles of triangle PQV, so angle PQV = 180 - a - (a+u) - (90-a) = 90-au. Note that this is equal to angle PP'Q'.
Now, the surface containing point V and circle PV is a cone. It's not a circular cone because the section cut by plane PV is oblique to the cone axis. A section perpendicular to the cone axis would have an elliptical cross-section. But note that plane CP' cuts the cone at the same angles, just in the opposite direction. Since plane PV cuts the cone in a circle, plane CP', with the same obliquity, should also cut the cone in a circle. Thus circle PV projects onto the plane as a circle, P'V'. The key to constructing stereographic projections is constructing any circle given its center and radius. Assume the
circle has radius r and its center is angular distance a from the point of tangency. If the circle is a unit circle, then
CP'=tan((a+r)/2) and CQ'=tan((a-r)/2).
The center of the circle on the sphere will not project as the center of the circle on the plane. The distance to the center of the projected circle is
(CP'+CQ')/2 = tan((a+r)/2) +tan((a-r)/2).
Since tan u + tan v = sin(u + v)/(cos u cos v) we can let
u = (a+r)/2 and v = (a-r)/2.
We can then write:
Radius of center = sin(((a+r)/2) + ((a-r)/2))/...
.. (cos((a+r)/2) cos ((a-r)/2) = sin a / (cos((a+r)/2) cos((a-r)/2)
We can also make use of the fact that cos u cos v = (cos(u+v) + cos(u-v))/2 to continue:
sin a /(cos((a+r)/2) cos((a-r)/2) =
· sin a /(cos(((a+r)/2)+((a-r)/2)) + cos(((a+r)/2)-((a-r)/2))/2) =
2sin a /(cos a + cos r) =
The formula for the radius of the projected circle differs only in the middle sign, which is negative instead of positive. The radius of the projected circle is (CP'- CQ')/2 =tan((a+r)/2) - tan((a-r)/2). Proceeding as above, we obtain radius = sin r /(cos a + cos r)
Thus:
Distance to center of projected circle = sin a /(cos a + cos r)
Radius of projected circle = sin r /(cos a + cos r)
Constructing a Stereonet Constructing Great Circles
For great circles, the radius is 90 degrees and cos r = 0. Thus the distance and radius formulas for the projected circle become:
Distance = tan a
Radius = 1/cos a
If we want to construct a stereonet in the standard orientation with the great circles like meridians of longitude, then the circle that represents longitude w will have its pole at
longitude w plus or minus 90. Thus the distance to the pole is -1/tan(w) and the center of the circle lies on the equator. The minus sign in the distance formula simply means that the center of the circle lies on the opposite side of the sphere from the meridian. The radius of the projected circle is 1/cos(w). The formulas suggest the simple construction at left. Linear dimensions are in red, angles in purple.
It is useful to introduce angle u, since 1/tan w =tan(90-w) = tan u. Measure angle u from the prime meridian as shown and draw SPC. Point C
is the center of the great circle. Alternatively, if the primitive circle is marked with degrees, simply measure off angles 2u and
2w as shown and construct SPC. For the great circles very close to the prime meridian, point C may be so far away it is impossible to plot. It's useful to have some formula that relates distance AO and angle w.
(AO is sometimes called the sagitta, from the Latin word for arrow, because arc NAS and line AO somewhat resemble a bow and arrow.) The formula is simple and follows directly from the construction of the projection: AO = tan (w/2).
Constructing Small Circles
For the small circles of the stereonet, a always equals 90 because the circles are centered on the pole. Thus, a circle of latitude l has radius 90-l. The distance to its center is 1/cos r= 1/sin l. Its radius is tan r = 1/tan l. The simple construction at left can be used to plot a small circle of latitude l. Draw OP making angle l with the equator. Draw PC perpendicular to OP. C is the center of the circle.
UNIV. OF WISCONSIN GREEN BAY: THE ORIGINAL FIGURES CAN BE FOUND ON THIS SITE.