STRAIN ELLIPSE


The equation of a circle with unit radius, and its centre at the origin is given by:
x2 + y2 = 1
If we deform this circle according to the general two dimensional linear transformation, the eq below can be derived:
[ (dx'-by')/(ad-bc)]2 + [(-cx'+ay')/(ad-bc)]2 = 1
x'2 (d2+c2) 2x'y' (bd+ac) y'2 (a2+b2)
-------------- - ------------- + --------------- =1
(ad-bc)2 (ad-bc)2 (ad-bc)2
Simplifying the constant terms,
Ax'2 -2B x'y' +Cy'2 =1
Which is an ellipse, the strain ellipse or finite strain ellipse with its centre at the origin. It can be shown that the principal strains are given by the quadratic equation which has positive roots:
(1+e1)2 or (1+e2)2=[(a2+b2+c2+d2)/2] ± { [(a2+b2+c2+d2)2 - 4(ad-bc)2]1/2}/2
and that they make angle q ' with x axis where q ' is given by:
tan 2 q '=[2(ac+bd)]/(a2+b2-c2-d2)
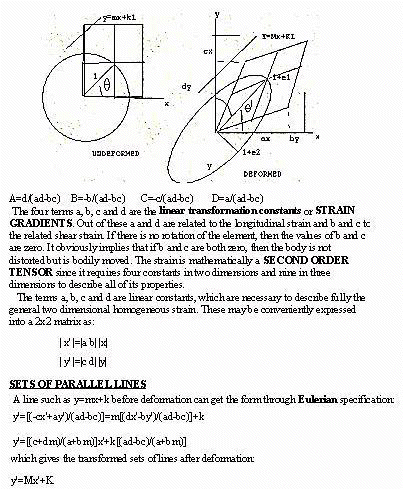
Just as the sides of the original square grid were rotated during two dimensional homogeneous strain, so is the line which becomes the major axis and the line that becomes the minor axis of the strain ellipse. These lines known as the PRINCIPAL STRAINS or PRINCIPAL AXES OF STRAIN can be shown to have made an angle before the deformation with the x axis, where is given by:
tan 2 q = [2(ab+cd)]/[a2-b2+c2-d2]
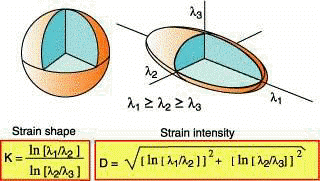
The ratio of the principal strains is called the ELLIPTICITY of the finite strain ellipse.
The principal axes of strain are therefore rotated through an angle ( q ' - q ) during the two dimensional homogeneous strain to become the Principal Strains. This angle designated by w (omega) is called the rotational component of strain:
w = q ' - q
The two dimensional strain is IRROTATIONAL only when b and c of the constants are equal and the matrix becomes symmetric, since q ' and q are the equal.
| a b |
| b d |