FLINN DIAGRAM
Flinn (1962), first suggested that the geometry of three-dimensional finite strain can be given in terms of five ellipsoids if the geological strain is unaccompanied by volume change or dilation. The ellipsoid 1 (extreme left) has two positive extensions equal, the lines of no finite longitudinal strain define helical loci; ellipsoid 2 (second from left) in which two positive extensions are unequal, the lines of no finite longitudinal strain are not strictly helical; ellipsoid 3 (centre) in which one of the principal strains is zero, one positive and the other negative, the lines of no finite longitudinal strain are not existent but only two circular planes exist; ellipsoid 4 (second from right) in which two extensions are negative but unequal and the third is positive, the loci of lines of no finite longitudinal strain are elliptic cones and finally ellipsoid 5 (extreme right) in which two extensions are negative and equal and the loci of lines of no finite longitudinal strain are circular cones making equal angles with both negative extension directions. For further details, please click here. The lower set of diagrams show equal area projections for five types of ellipsoids with the areas of poles to planes extended separated from those of poles to planes contracted (hatched). Flinn's equations in terms of the angles between the cones of lines of no finite longitudinal strain in the three principal planes of the finite deformation ellipsoid are given below. XZ plane or l1l3 plane: yxz =cos -1 [(a-2/3b2/3 - b2 )/(a-1 - b2 )]1/2 YZ plane or l2l3 plane: yyz=cos-1 [(a-2/3b2/3- b2 )/(1 -b2 )]1/2 XY or l1l2 plane: yxy =cos-1 [ (a-2/3b2/3 -1)/(a-1 - 1 )]1/2 As you know a=(1=e1)/(1+e2) and b=(1+e2)/(1+e3). In terms of the quadratic extensions, the positions of cones of or planes of e=0 can be given by the equations: in XY or l1l2 plane : jxy=tan-1{ [l2(l1-1)]/[l1(1-l2)]}1/2 in XZ or l1l3 plane: jxz=tan-1{[l3(l1-1)]/[l1(1-l3)]}1/2 in YX or l2l3 plane: jyz=tan-1{[l3(l2-1)]/[l2(1-l3)]}1/2 The values of X, Y and Z or of 1+e1, 1+e2 and 1+e3 can be given in terms of a an b by the following equations as long as the deformation is volume conserving. 1+e1 or X =a2/3.b1/3 1+e2 or Y =a-1/3.b1/3 1+e3 or Z =a-1/3.b-2/3 so that the product X.Y.Z always equals unity.
|
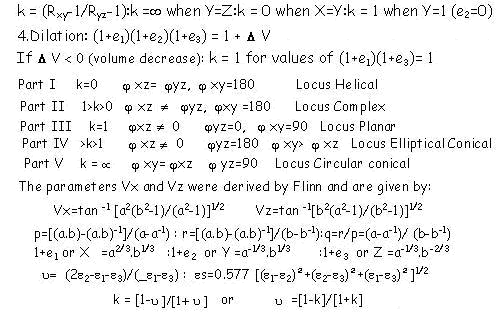 |