LAYER PARALLEL STRAIN
Component of strain during folding that causes change in thickness of the buckling layer within limits of the threshold critical limb dip. Dependent on the viscosity contrast between layer and matrix
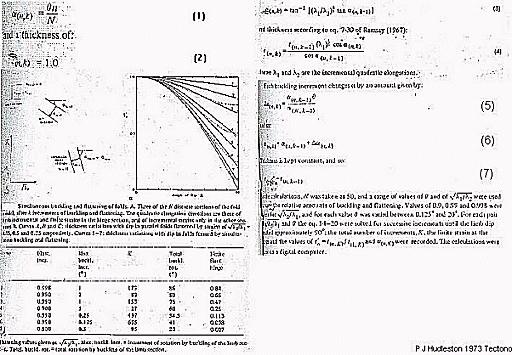
SIMULTANEOUS BUCKLING AND FLATTENING MODEL
Although De Sitter (1964) and Ramsay (1967, p.4ll)recognise that in general unlimited shortening of an actively folding layer maintaining a parallel form is impossible, the production, by a buckling process, of a parallel fold which then becomes homogeneously flatlened seems equally unlikely, since the initial buckling necessitates a competency difference between the layer and the enclosing medium which must disappear at some later stage for the fold to flatten in a true homogeneous manner.
It seems likely that where the ductility contrast is low an actively folding layer will deform by a combination of a buckling and a flattening process. A simple process that simulates the simultaneous buckling and flattening of a competent layer is described below.
The fold is represented by a large number, N, of discrete sections between hinge and inflexion points, each section defined selely by its dip, and its thickness. Folding is initiated with a buckling increment to give the nth of the N sections a dip as in eq 1 and 2.In these, k =I for the first increment, and theta = the maximum rotation of the limb for each buckling increment.
This is now followed by tbe first increment of flattening, and then alternate increments ofbuckling and flattening are successively added. k increases by 1 for each increment of either buckling or flattening. Each flattening increment of pure shear changes theta according
to standard formula (e.g. Ramsay, 1967, eq. 3 - 34), eq 3-7 here.
On plotsof t' against theta, the resultant geometry of the folds varies between parallel (lB pure buckling) and similar (involving large components of flattening); the plots form a farmily of non-intersecting curves that differ systematically from those relating t' to alpha
flattenedarallel folds, the difference between these two sets of curves is most marked for very high limb dips, and very slight at low dips. Representative curves are plotted in Fig. where this comparison may be made. The folding process is independent of the shape of the layer bounding surfaces, which (arbitrary: the state of strain within the layer is subject only to the geometrical restraints imposed by the values of dip and thickness and can therefore be accommodated in
number of ways (not all of which are equally likely). It must be stressed that there is no mechanical basis for choosing this model, and the the process, will certainly be more complex. However, the model has proved useful, in a tentative way, in the interpretation of plots of t' against alpha for natural and experimentally produced folds (Hudleston, 1973a, 1973b). The reason why many folded competent rock layers appear to show a geometrical relationship between t' and a expected of ideal flattened parallel folds (see Ramsay, 1967;Mukhopadhyay,1965)may be due to the rheological contrast decreasing or vanishing during deformation.
The resistance to continued buckling in the layer, imposed by the enclosing medium, increasing as the fold tightens and the material of the medium becomes extruded from the regions between the limbs of the buckling layer (see Chapple, 1968). The competent layer may then be forced to take up further deformation by flattening.
A"buckling and flattening" process resulting in a fold whose geometry is scarcely indistinguishable from that produced by homogeneously flattening a parallel fold. The model proposed here is compatible with explanation for low dip values. An explanation accordingly is most unlikely to hold as a general rule, and some combination of the reasons given may account for the observed geometry of many natural folds.
This model was developed by Hudleston by imparting infinitesimally small increments of layer parallel strain (increase in thickness) and buckling strain (increase in limb dip). The model loses significance when fold limbs attain dips greater than 20 degrees when in most folds the layer parallel shortening stops. But how much shortening has taken place before this stage is important. The significant point shown in figure is that folds which formed by considerable layer parallel strain in early stages can be distinguished after flattening from true parallel folds (with buckle strain predominent) for high limb dips on t'/limb dip plot in that the curvatures for lines differ in their straightening out in case of the fold that suffered layer parallel strain and differ from ideal theoretical curves for 1C folds formed by homogeneous flattening.