 |
| CHEVRON FOLDS, THEORY
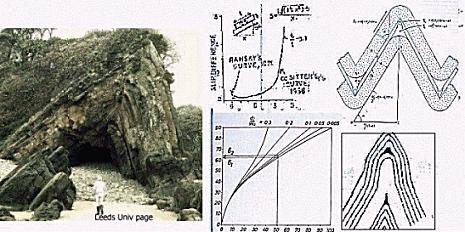
These are characterized by very long limbs and very narrow hinges (Figure ) and most of the naturally developed chevron folds have an interlimb angle around 60°. These folds develop in typical turbidite flysch sequences of alternating competent and less competent layers in which the thickness of competent layers does not vary across the complex. de Sitter (1958) developed a chevron fold model consisting of layers of identical mechanical properties sliding over each other with no internal deformation. The slip increases with increasing deformation or shortening along layers until at some stage no further slip is possible and the structure locks. Further deformation is taken by hinge thickening and limb thinning as shown with support from model experiments by Behzadi and Dubey (1981). Ramsay (1974) modified de Sitter's model from the natural observations on chevron folds and showed that (top left, figure below) the slip function has a negative value in the initial stages but it soon takes positive values and the limb dip or percentage shortening at which this occurs is determined by the thickness/length ratio of layers involved in buckling. length ratio of the layers involved in buckling. Chevron folds are typical flexural slip folds and therefore all deformation occurs by layer-parallel shear.The chevron fold model is geometrically unstable if the thickness of competent layers varies across the complex. However, the variation in the thickness of less competent layers does not affect the formation of chevron folds. Shear strains are high in competent layers during the initial stages but gradually decrease. During advanced stages of folding the shear strains become high in less competent layers and this produces some anomalous structures associated with chevron folds (see later). For ideal chevron folds to develop, a threshold value of shear strain must be attained and this is in fact dependent upon the t/l ratio (where t is the thickness and 1 the length of the competent layer) and mechanical properties of competent 1ayers. Once these conditions are fulfilled, the folding of chevron style is accomplished rapidly. The shear stresses along layers decrease with progressive shortening. The percentage shortening, the limb dip a and t/l are related by 1+e=(1+t/l)cos a+t/l sin aas is apparent from bottom left part of figure above in which these relations are graphically recorded and supported by figures to the right. The geometry of chevron folds is typically of subclass 1B but the less competent layers may show class 3 geometry with divergent isogon fold style. In chevron folds, the competent layers do not undergo any significant internal deformation. But the less competent ones do undergo and show pronounced changes more particularly in hinge areas but strains within the limbs are low suggesting deformation by simple shear. Slickensided fibrous growth on limbs and extension veins indicate differential displacement in a direction normal to hinge lines. |