| COMPRESSIBILITY |
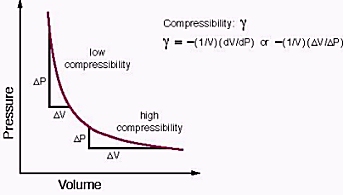 |
The terms compressibility and incompressibility describe the ability of molecules in a fluid to be compacted or compressed (made more dense) and their ability to bounce back to their original density, in other words, their "springiness." An incompressible fluid cannot be compressed and has relatively constant density throughout. Liquid is an incompressible fluid. A gaseous fluid such as air, on the other hand, can be either compressible or incompressible. Generally, for theoretical and experimental purposes, gases are assumed to be incompressible when they are moving at low speeds--under approximately 220 miles per hour. The motion of the object traveling through the air at such speed does not affect the density of the air.
In thermodynamics and fluid mechanics, compressibility is a measure of the relative volume change of fluid or solid as a response to a pressure (or mean stress) change.
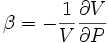
where V is volume and P is pressure. The above statement is incomplete, because for any object or system the magnitude of the compressibility depends strongly on whether the process is adiabatic or isothermal. Accordingly we define the isothermal compressibility as:
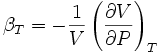
where the subscript T indicates that the partial differential is to be taken at constant temperature. The adiabatic compressibility as:
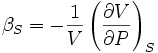
where S is entropy. For a solid, the distinction between the two is usually negligible.
The inverse of the compressibility is called the bulk modulus, often denoted K. That page also contains some examples for different materials.
The term "compressibility" is also used in thermodynamics to describe the deviance in the thermodynamic properties of a real gas from those expected from an ideal gas. The compressibility factor is defined as
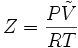
where P is the pressure of the gas, T is its temperature, and V is its molar volume. In the case of an ideal gas, the compressibility factor Z is equal to unity, and the familiar ideal gas law is recovered:
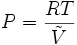
Z can, in general, be either greater or less than unity for a real gas.
The deviation from ideal gas behavior tends to become particularly significant (or, equivalently, the compressibility factor strays far from unity) near the critical point, or in the case of high pressure or low temperature. In these cases, an alternative equation of state better suited to the problem must be utilized to produce accurate result
Compressibility is a geological term used to quantify the ability of a soil to reduce in volume with applied pressure. It is an important concept in geotechnical engineering in the design of certain structural foundations. For example, the construction of high-rise structures over underlying layers of highly compressible bay mud poses a considerable design constraint, and often leads to use of driven piles or other innovative techniques.