ELASTICITY, ISOTROPIC,
ANISOTROPIC, HOOKEAN
Isotropic materials are those that have the same value for a given
property in all directions.Anisotropic materials are those that have
different values for a given property in different directions.
Types of deformation:Permanent, Recoverable:
Elastic response
Viscous response
Plastic response
Derived response models:
Mechanical combinations of
elastic, viscous and plastic response
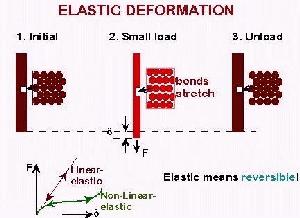
Elastic Response
Strain is recoverable instantaneously
Response to stress is instantaneous
The relationship between stress and strain is linear
For a normal stress, s
, producing an extension, e
, the relationship is given by the equation: s
= Ee
where the constant of proportionality, E, is call Young's modulus. This
equation is called is Hooke's Law
Note that E and all of the other elastic moduli described below have
the units of stress, because strain is dimensionless
Mechanical Analog for
Hookian Elastic Materials
Extension of a spring, note that:
strain-time indicates instantaneous response to stress
strain is also instantaneously recoverable
stress-strain relationship is linear
Other Elastic Responses
For dilation, the constant of proportionality is called the bulk
modulus, K, where: s
H = K (D
V/V)
For a shear stress, s
S , the constant of proportionality between shear stress and shear
strain (g)
is called the shear modulus, G, where: s
S = Gc
(The shear modulus is sometimes called the modulus of rigidity )
Poisson's ratio ( n
) is another property of an elastic material and is equal to the ratio of
lateral contraction to longitudinal extension during tensional loading
Relationships among elastic constants:
G = E/2(1+ n )
= 3K(1-2n )/2(1+n
)
Viscous Response
Newton's concept of fluid viscosity: fluid
material
Laminar flow occurs in the fluid between rigid plates as the plates
slide over one another
The fluid exerts an internal frictional resistance to the movement
which is called the viscosity of the fluid
Because of this resistance, force or shear stress must be continually
applied to keep the plate moving
For such fluids, the strain is proportional to the stress and the time
it acts, and is inversely proportional to the viscosity, h
, of the fluid
Viscous Response
The strain is proportional to the stress and the time it acts, and is
inversely proportional to the viscosity, h
, of the fluid
This relationship is given by the following equations for normal stress
and shear stress:
e = s
t/h or s
= h e
/t Þ s
= h de
/dt
similarly s s =
h dg
/dt
Note that the longer the stress is applied, the greater the strain for
a given stress.
Note that the shorter the time involved, the greater the stress
required to produce a given strain.
Viscous Response
A material that exhibits this property is said to be a Newtonian fluid
In a Newtonian fluid, the viscosity is constant for all rates of the
application of stress or rates of strain - Figure (a) below
However, there are fluids whose viscosity varies as a function of
strain rate ‑
these are called non-newtonian fluids - Figure (b) below
Most highly viscous fluids are non-newtonian
The change in viscosity as a function of strain rate is generally
attributed to structural changes within the material
It may be that non-newtonian viscous behavior is a close approximation
to that of real rocks at depth
Geological
Implications of Viscous Behavior
The slower the strain rate the lower the stress required for
deformation.
For very low strain rates (e.g. over geologic time), low stresses may
be able to deform even very viscous fluids. This has major geological
implications
Mechanical Analog of
Viscous Response
A mechanical analog for viscous behavior is the dashpot, a loose piston
moving through a cylindrical tube whose walls are lubricated by some
fluid. e.g. a hydraulic cylinder on a rowing machine. Note that:
Strain is time dependent (the longer the time, the more the strain)
(contrast this with elastic behavior)
The stress-strain rate relationship is linear
Plastic Response
An ideal plastic body does not yield until some critical stress ( s
c) is reached.
Most materials that approach being plastic exhibit elastic properties
below this point so this critical stress is at the elastic limit or yield
point of the material
Mechanical analog - a sliding mass (where s
c is analogous to frictional resistance)
Plastic Response
Beyond the yield point a plastic material strains continuously and
permanently
The plastic material flows but is different from viscous materials
since it has some fundamental strength (the critical stress) which the
viscous fluid does not have
Also, in ideally plastic materials, the strain takes place in localized
regions where the critical stress has been reached, whereas, ideally
viscous materials show deformation throughout the material wherever a
deviatoric stress is present
Elastico-Plastic
Response
As noted above, most materials that display plastic behavior display
elastic behavior below the critical stress
Such materials are said to be elastico ‑plastic
(sometimes called a Prandtl modal) and can be characterized with an analog
model of a spring attached to a sliding mass
The mass requires a critical stress to begin moving against friction,
but a certain amount of elastic strain is sustained by the spring before
the critical stress is reached
Once the mass begins to move (strain) the applied stress has exceeded
the critical stress and a constant stress keeps it moving (straining)
This is an example of a derived response model - one that includes a
combination of one or more of the simple or fundamental models (elastic,
plastic, viscous) in either series or parallel combinations
Derived Response
Models
Most real materials do not respond to stress in a manner exactly like
any of the three elementary responses
In many cases, combinations of these models do approach the behavior of
real rock materials
Other derived response models
Plasticoviscous reponse
Firmoviscous response
Elasticoviscous response
Plasticoviscous
Response (Bingham model)
Analog ‑
dashpot plus a sliding mass in parallel
Visco-Elastic
Response
(Kelvin model)
Also called a firmoviscous response
Analog ‑spring
and dashpot in parallel
The dashpot causes the elastic response to be delayed so that the
elastic (recoverable) part of the response is time dependent both on
loading and unloading
Stress ‑strain
relationship is linear with no fundamental strength for the material
Elasticoviscous
Response (Maxwell model)
Analog ‑
spring plus dashpot in series
Response is instantaneous and strain may increase infinitely
Recovery of the elastic strain is instantaneous, but the viscous strain
is not recovered
|