HOSSACK DIAGRAM

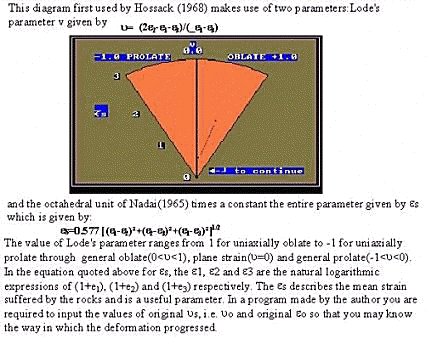
HSU or HOSSACK DIAGRAM

This diagram first used by Hossack (1968) makes use of two parameters:Lode's parameter v given by     

                               u=  (2e₂-e₁-e₃)/(_e₁-e₃) 

and the octahedral unit of Nadai(1965) times a constant the entire parameter given by es which is given by:
                  es=0.577 [(e₁-e₂)²+(e₂-e₃)²+(e₁-e₃)²]^1/2

The value of Lode's parameter ranges from 1 for uniaxially oblate to -1 for uniaxially prolate through 

general oblate(0<u<1), plane strain(u=0) and general prolate(-1<u<0). In the equation quoted above for es, the e1, e2 and e3 are the natural logarithmic expressions of (1+e₁), (1+e₂) and (1+e₃) respectively. The es describes the mean strain suffered by the rocks and is a useful parameter. In a program made by the author you are required to input the values of original us, i.e. uo and original eo so that you may know the way in which the deformation progressed.

The relationship between Lode's parameter, u    and Flinn's parameter k can be given by:

                k = [1-u  ]/[1+ u   ]

   or          u  =[1-k]/[1+k]

The comparative table could be as given below:

Ellipsoid type       e₁      e₂       e₃       k            u                                 Quadratic Extensions

Uniaxially oblate  +ve   +ve     -ve       0             1.0     e₁=e₂                     l₁=l₂>1>l₃         

General Oblate    +ve   +ve    -ve      >0,<1       <1,>0   e₁¹  e₂                l₁>l₂>1>l₃

Plane Strain         +ve    0       -ve       1.0          0.0                                    l₁>1=l₂>l₃

General Prolate    +ve  -ve     -ve     >1, < µ        <0, >-1.0    e₂ ¹  e₃      l₁>1>l₂>l₃

Uniaxially Prolate +ve  -ve     -ve         µ              -1.0            e₂=e₃         l₁>1>l₂=l₃ 

   The relationship between Lode's parameter can be expressed by the equation:

            k=(1- n  )/(1+n  )

   or       n=(1-k)/(1+k)