| HUDLESTON'S EXPERIMENTS
On the basis of his experimental studies Hudleston (1973) concluded that W/t and maximum layer shortening values were consistent for a given viscosity contrast despite the duration of the experiment and the length of time permitted to elapse before beginning of each experiment. He found that the grid lines deflected sharply in trend at the layer edges. He attributed this to change in viscosity contrast during the experiment and diffusion across the layer matrix interface. The greater the diffusion, less sharp are the deflections of trend lines. He also concluded that before the limb dips of 15 are achieved, there is considerable layer parallel strain and very little change in the arc length (see figures with b3/b1 plots), the folding layer shortens rather as a flat plate. The process of wavelength selection proposed by Sherwin and Chapple probably does not begin until this critical limb dip stage is achieved. After this stage the W/t ratio is believed to be fixed and is independent of the amplification rate. But the actual critical value of limb dip probably depends upon the "flatness" of the layer. Thus it may also be concluded that major changes in the length of layers occur only during initial stages of folding. He produced folds in layers with ml/m2 as low as 5.5. 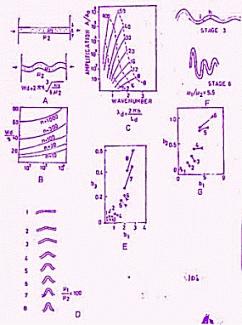
Hudleston (1973) also subjected the folds to the harmonic or Fourier analysis and found that the ratio b3/bl steadily increased with progressive development of folds. He found that for most of the experimentally produced folds, the ratio b3/bl at any stage is less for the outer than for the inner arc. The increasing ratios suggest modification of initial sine waves to more complex parabolic or semi-elliptic shapes HUDLESTON'S PARAMETER
The parameter phi by Hudleston This parameter was developed by Hudleston (1973), chiefly to avoid measurements of orthogonal and axial plane thickness which is a time consuming and tedious procedure. It is designated as f and is here called Hudleston's parameter. It is the angle between the dip isogon for a particular value of and a normal to the tangents for the same value. If the isogon is deflected anticlockwise from the normal in going from inner to outer arc, it is taken to be positive in sign and if it is deflected clockwise from the normal, it is taken to be negative. fig. given shows a plot of f /a for fold drawn. Left half of the diagram is for the left limb of a fold, while right half is for the plots of right limb of a fold. f is taken to be positive for left limbs of synforms and right limbs of antiforms while it is taken as negative for right limbs of synforms and left limbs of antiforms. Folds of each class occupy different fields on this graph. a is positive for left limbs of antiforms in 1A field, but negative for right limbs. f takes a value of zero on both limbs of 1B folds since isogons in 1B folds are perpendicular to layer surfaces and therefore normal to the two tangents for two adjacent surfaces. f is positive for the right limbs of antiforms in subclass 1C folds but negative for the left limbs of antiforms, a situation reverse for that of class 1A folds. f equals a in similar folds. It is negative on left limbs of antiforms, and positive for their right limbs. f is greater than a in class 3 folds. It is negative for left limbs of antiforms and positive for right l imbs. To sum up, in subclass 1C, classes 2 and 3 the values of f and a both are negative for left limbs of antiforms and right limbs of synforms. Conversely, in subclass lC, classes 2 and 3, f and a are both positive for the right limbs of antiforms and left limbs of synforms (fig. 4.13). One advantage of f/a plot is that it straightens the line of class 2 or similar folds which is otherwise curved in t'/a plot, the value of t' being equal to cos a ; or in 1B folds on a T'/a plot, the value of T' being equal to sec a. As shown by Hudleston (1973), there is generally no direct relationship between t' and f for a given value of a . But for the first derivative of the ratio dt'/da and the increment of t' and increment of approach zero in dt'/da =-t'a tan f or f=tan-1 [-1/t'a.dt'/da ]
|