STRESS, EFFECTIVE
High pore pressure tends to promote brittle behavior of materials. It is important to understand that the fluid is not a lubricant but it reduces the value of normal stress needed for failure. The pore pressure reduces the effective confining pressure on the material as well as the effective load pressure. This is the effective stress needed to cause failure.
STRESS, DUE TO OVERBURDEN
If all three of the principal axes are of equal magnitude, then the ellipsoid simplifies to a sphere, and each of the infinite number of stress vectors are equal.
This particular type of stress is termed Hydrostatic stress. Under these conditions, none of the infinite plans feel a shear stress, and the material may undergo volume and/or mineralogical changes, but no deformation occurs. This type of stress is commonly experienced by deeply buried rocks.
STRESS, ELLIPSOID
A component of stress in any direction is often called the stress in that direction. However, stress at a point, as noted earlier, is really a tensor quantity. The vector quantity representing the magnitude and direction of stress in any given direction is called a traction.
The stress acting on a small element of a body is the aggregate of all tractions in all directions acting on that element. When the tractions in all directions acting on an element are equal in magnitude, the stress is said to be isotropic. Hydrostatic pressure, for instance is an isotropic stress because a fluid is normally stressed equally in all directions. The locus of all tractions acting equally on a point forms a sphere.If the stress is anisotropic, the tractions are not all equal, but in order to maintain dynamic equilibrium they must be such that each traction is balanced by another that is equal in magnitude and opposite in sense. The locus of all tractions acting on an anisotropically stressed point forms an ellipsoid that we call the stress ellipsoid.The major and minor semiaxes of this ellipsoid are the greatest and least principal stresses (
s1 & s3). The intermediate semiaxis which is normal to the s1-s3 plane is the intermediate principal stress s2.The Stress Ellipsoid
A component of stress in any direction is often called the stress in that direction. However, stress at a point, as noted earlier, is really a tensor quantity. The vector quantity representing the magnitude and direction of stress in any given direction is called a traction.
The stress acting on a small element of a body is the aggregate of all tractions in all directions acting on that element. When the tractions in all directions acting on an element are equal in magnitude, the stress is said to be isotropic. Hydrostatic pressure, for instance is an isotropic stress because a fluid is normally stressed equally in all directions. The locus of all tractions acting equally on a point forms a sphere.
If the stress is not isotropic - that is, if it is anisotropic - the tractions are not all equal, but in order to maintain dynamic equilibrium they must be such that each traction is balanced by another that is equal in magnitude and opposite in sense. The locus of all tractions acting on an anisotropically stressed point forms an ellipsoid that we call the stress ellipsoid.
The major and minor semiaxes of this ellipsoid are the greatest and least principal stresses (s 1 & s 3). The intermediate semiaxis which is normal to the s 1- s 2 plane is the intermediate principal stress s 2.
. Classification of stress at a point by ellipsoid type: 1. Triaxial stress s1=>s2=> s3 does not equal 0 (ellipsoid or sphere); 2. Biaxial stress s1=> s2 does not equal 0, s 3=0 (ellipse); 3. Uniaxial stress s 1>0, s 2=s 3=0 (vector, not a tensor); 4. General triaxial stress s1>s 2>s 3 (ellipsoid, no equalities); 5. Hydrostatic stress s 1=s 2=s 3 (sphere)
STRESS, MEAN
Mean stress =(s1+s2+s3)/3 = sm (a hydrostatic stress). Confining pressure alone does not cause a change in size or shape of a material unless the rock is highly porous. Once the porosity of the material is reduced, little additional deformation is caused by confining pressure alone. It is differential pressure (or differential stress) that causes deformation. A measure of this differential stress is the deviatoric normal stress on a plane:sd =s1-sm or the principal deviatoric stresses: s1d=s1-sm ;s2d=s2-sm ;s3d=s3-sm.
The deviatoric shear stress has the same value as the shear stress and is independent of the mean stress. The sign of the deviatoric stress is an indication of the relative effect of a given normal stress. For instance, if the sign of a deviatoric stress is negative, even though the stress is a compressive stress, its relative effect (i.e.. relative to the other normal stresses acting on a point) is tensile. The least principal stress (s 3) is always a negative deviatoric stress and can be thought of as a relative tensile stress, even in a situation where all of the principal stresses are positive.
STRESS, TRIAXIAL
Triaxial Stress is where all three of the principal axes are non-zero. s S max = (s 1 - s 3)/2
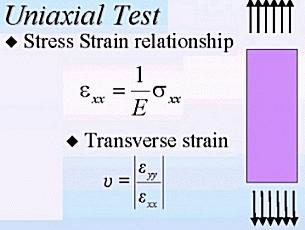
STRESS, UNIAXIAL
Uniaxial Stress is where only one of the principal axis is non-zero.
E. Principal stresses
In the development of the equations for s n and s S in a general 2D stress state, we considered general orientations of the stresses with respect to our x and y axes, i.e.
As a result each general stress vector had a normal and shear component parallel to x and y. Our only assumption was that there is static equilibrium, so s xy = s yx.
We could have chosen our coordinate system x,y such that only normal stresses where parallel to x and y, i.e.:
In this system, the planes perpendicular to x and y have no shear stresses acting on them.
IT IS ALWAYS POSSIBLE TO CHOOSE AN ORTHOGONAL COORDINATE SYSTEM X, Y SUCH THAT THE PLANES NORMAL TO X AND Y HAVE NO SHEAR STRESS DIRECTED ACROSS THEM.
Or we can state:
There exist 2 mutually perpendicular planes in plane stress (3 in 3D stress) for which shear stress is zero and the normal stresses are either a maximum or a minimum.
The normal stresses in such an orientation are called the principal stresses and are given the symbols s1 & s 2 where ( s1 > s 2) or in 3D (s 1 > s 2 > s 3).