SHEAR ZONES, GENERAL CONCEPTS
Shear Zones
(a) Changes in grain size, with grain size sensitive deformation mechanism or mechanism switch
(b) Influx of fluids and enhanced permeability during deformation (dilatancy) (c) Shear zones often associated with retrograde metamorphism
(d) Hydrolitic weakening in quartz
(c) Previous brittle faulting or ductile shear in extension of brittle fault zone
(d) Shear heating giving thermal weakening
(e) Transformation plasticity- metamorphic reaction enhances deformation and reaction softening where a new metamorphic mineral is softer or finer grained than the old one
(f) Geometric weakening -Development of preferred orientations and development of grain shape foliation & domainal fabric and also rearrangement of mineral distribution & shape
(g) Recrystallisation
The fig is after Jessel et al.
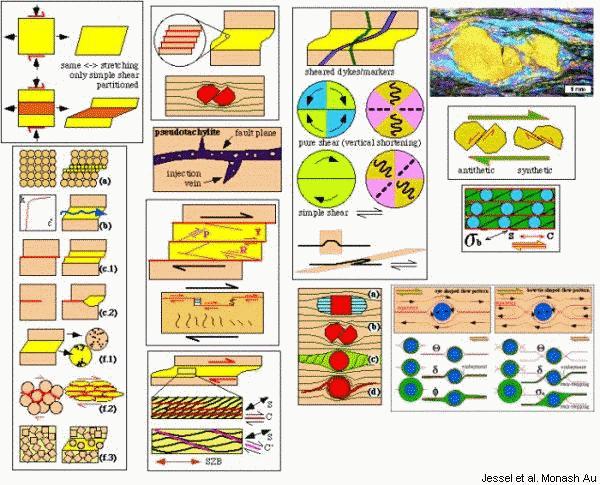
SHEAR ZONES
These are subplanar narrow parallel sided zones within which the amount of strain is considerably greater than the host rock. In other words, the stresses acting on rocks cause ductile deformation that is localized. The zones are those in which strain softening predominates and grain size reduces considerably from that of the original rock in case there are not too many fluids or hyperfusibles that may not allow linear viscous deformation. A marker such as an aplite vein or mafic dyke in the original rock prior to shearing may undergo marked change in orientation with or without folding or boudinage depending upon its orientation. Based on the angular relationship between the dyke or vein within and outside the shear zone with the direction of shear, the amount of shear strain, and therefore the total displacement across the zone can be easily computed. Such veins or dykes also help in computing the volume change during deformation.
SHEAR ZONES IN MAGMATIC ROCKS
Typically, there is a strong tendency towards non-coaxial (simple shear) deformation within the shear zone. This is because of compatibility of strain rate and normal stress across a plane equal, parallel stretching across a plane equal. Simple shear component can be partitioned by factorization.