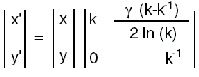Vorticity

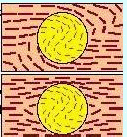
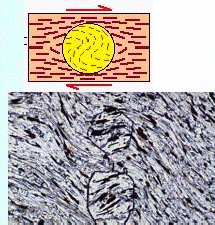
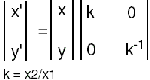
Structural elements such as planes or lines or spherical or ellipsoidal or inequant objects often undergo rotation or rigid body rotation owing to pulsating deformation paths. Figures below show the rotation of an equant porphyroblast together with the fabric, and rotation before the development of fabric under coaxial and noncoaxial deformation and the growth on a preexisting folded fabric. 
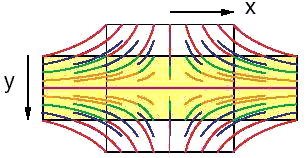
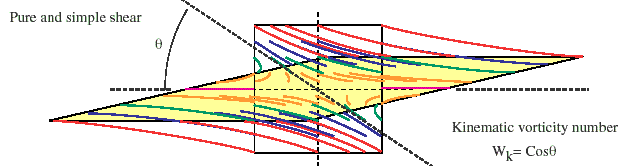
Flow lines represent the path followed by material particles or material lines during the progressive deformation. The kinematic vorticity number or Wk (Truesdel 1954, Ramberg 1975, Ghosh and Ramberg, 1976, Ghosh 1987 for Sr) vanishes or becomes zero for irrotational deformtion and is unity for rotational deformation exclusively by simple shear. For any deformation which is by combination of pure and simple shear the value of Wk is greater than zero but less than unity. 
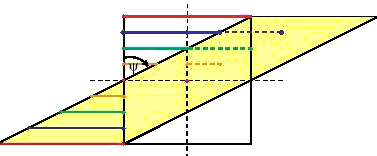
If Wk=0 then the particle paths or velocity field consists of a family of hyperbolae asymptotic to the two flow apophyses. If Wk=1, then the velocity field is purely defined by straight parallel lines. However, if the value of Wk is 1>Wk>0 then the deformation path is a combination of two, one for pure shear part and another for the simple shear component, i.e. of straight line segments and hyperbolae but asymptotic to the two acute ( -ve) and obtuse ( +ve) flow apophyses.
In the figure above, the 1>Wk>0. The ISAs make an angle with each other whose cosine is a measure of Wk. This was also simulated using equations given by Ramberg (1975) and the output is shown 
However, the relations in that simulation are more complex.
As shown by Ghosh and Ramberg, Sr or the rate of pure to simple shear will determine how fast the particle will rotate relative to the matrix given an axial ratio that is constant. Or the axial ratio large, the particle will have the rate of rotation as fast as the matrix markers.
Using the software GhoshFlow written by R H Holcombe, the author has made the three animations that follow on the next two pages. In the first case, the Wk=0 and the ISA are normal and the ellipticity gradually increases. The shear strain is zero. In the second animation, Wk=1, the shear strain gradually increases but the ISA in both are above the line of Wk=0. In the third animation, Wk=0.45, the ISA lie eqaully on both sides of Wk=0 axis, the shear strain and ellipticity gradually increase as the deformation progresses by a combination of both pure shear and simple shear.
In case 1, Sr=Infinity, in the second case Sr=0 and in the third case,Sr equals 0.99 or is nearly unity. These are but ideal cases, but one may alter the values of Wk and the axial ratio R and obtain the results similar to those obtained by Ghosh(1975) and by Ghosh and Ramberg(1976).